Cyclic Redundancy Codes (CRCs) are among the best checksums available to detect and/or correct errors in communications transmissions. Unfortunately, the modulo-2 arithmetic used to compute CRCs doesn't map easily into software. This article shows how to implement an efficient CRC in C or C++.
Download Barr Group's Free CRC Code in C now.
A CRC is a powerful type of checksum that is able to detect corruption of data that is stored in and/or transmitted between computers. If you suspect data corruption has led to a system failure, Barr Group can help by performing forensic analysis and reverse engineering services.
Generally speaking, CRCs are most efficiently calculated in dedicated hardware. However, sometimes you must compute a CRC in software, for example in a C or C++ program that will run in an embedded system.
CRC Math in C
I'm going to complete my 3-part discussion of checksums by showing you how to implement a CRC in C. I'll start with a naive implementation and gradually improve the efficiency of the code as I go along. However, I'm going to keep the discussion at the level of the C language; further steps could be taken to improve the efficiency of the final code by moving into the assembly language of your particular processor.
For most software engineers, the overwhelmingly confusing thing about CRCs is their implementation. Knowing that all CRC algorithms are simply long division algorithms in disguise doesn't help. Modulo-2 binary division doesn't map particularly well to the instruction sets of off-the-shelf processors. For one thing, generally no registers are available to hold the very long bit sequence that is the numerator. For another, modulo-2 binary division is not the same as ordinary division. So even if your processor has a division instruction, you won't be able to use it.
Before writing even one line of code, let's first examine the mechanics of modulo-2 binary division. We'll use the example in Figure 1 to guide us. The number to be divided is the message augmented with zeros at the end. The number of zero bits added to the message is the same as the width of the checksum (what I call c); in this case four bits were added. The divisor is a c+1-bit number known as the generator polynomial.
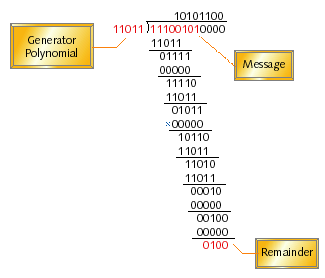
Figure 1. An example of modulo-2 binary division
The modulo-2 division process is defined as follows:
- Call the uppermost c+1 bits of the message the remainder
- Beginning with the most significant bit in the original message and for each bit position that follows, look at the c+1 bit remainder:
- If the most significant bit of the remainder is a one, the divisor is said to divide into it. If that happens (just as in any other long division) it is necessary to indicate a successful division in the appropriate bit position in the quotient and to compute the new remainder. In the case of modulo-2 binary division, we simply:
- Set the appropriate bit in the quotient to a one, and
- XOR the remainder with the divisor and store the result back into the remainder
- Otherwise (if the first bit is not a one):
- Set the appropriate bit in the quotient to a zero, and
- XOR the remainder with zero (no effect)
- Left-shift the remainder, shifting in the next bit of the message. The bit that's shifted out will always be a zero, so no information is lost.
- If the most significant bit of the remainder is a one, the divisor is said to divide into it. If that happens (just as in any other long division) it is necessary to indicate a successful division in the appropriate bit position in the quotient and to compute the new remainder. In the case of modulo-2 binary division, we simply:
The final value of the remainder is the CRC of the given message.
What's most important to notice at this point is that we never use any of the information in the quotient, either during or after computing the CRC. So we won't actually need to track the quotient in our software implementation. Also note here that the result of each XOR with the generator polynomial is a remainder that has zero in its most significant bit. So we never lose any information when the next message bit is shifted into the remainder.
Bit by Bit
Listing 1 contains a naive software implementation of the CRC computation just described. It simply attempts to implement that algorithm as it was described above for this one particular generator polynomial. Even though the unnecessary steps have been eliminated, it's extremely inefficient. Multiple C statements (at least the decrement and compare, binary AND, test for zero, and left shift operations) must be executed for each bit in the message. Given that this particular message is only eight bits long, that might not seem too costly. But what if the message contains several hundred bytes, as is typically the case in a real-world application? You don't want to execute dozens of processor opcodes for each byte of input data.
#define POLYNOMIAL 0xD8 /* 11011 followed by 0's */
uint8_t
crcNaive(uint8_t const message)
{
uint8_t remainder;
/*
* Initially, the dividend is the remainder.
*/
remainder = message;
/*
* For each bit position in the message....
*/
for (uint8_t bit = 8; bit > 0; --bit)
{
/*
* If the uppermost bit is a 1...
*/
if (remainder & 0x80)
{
/*
* XOR the previous remainder with the divisor.
*/
remainder ^= POLYNOMIAL;
}
/*
* Shift the next bit of the message into the remainder.
*/
remainder = (remainder << 1);
}
/*
* Return only the relevant bits of the remainder as CRC.
*/
return (remainder >> 4);
} /* crcNaive() */
Listing 1. A naive CRC implementation in C
Code Cleanup
Before we start making this more efficient, the first thing to do is to clean this naive routine up a bit. In particular, let's start making some assumptions about the applications in which it will most likely be used. First, let's assume that our CRCs are always going to be 8-, 16-, or 32-bit numbers. In other words, that the remainder can be manipulated easily in software. That means that the generator polynomials will be 9, 17, or 33 bits wide, respectively. At first it seems we may be stuck with unnatural sizes and will need special register combinations, but remember these two facts:
- The most significant bit of any generator polynomial is always a one
- The uppermost bit of the XOR result is always zero and promptly shifted out of the remainder
Since we already have the information in the uppermost bit and we don't need it for the XOR, the polynomial can also be stored in an 8-, 16-, or 32-bit register. We can simply discard the most significant bit. The register size that we use will always be equal to the width of the CRC we're calculating.
As long as we're cleaning up the code, we should also recognize that most CRCs are computed over fairly long messages. The entire message can usually be treated as an array of unsigned data bytes. The CRC algorithm should then be iterated over all of the data bytes, as well as the bits within those bytes.
The result of making these two changes is the code shown in Listing 2. This implementation of the CRC calculation is still just as inefficient as the previous one. However, it is far more portable and can be used to compute a number of different CRCs of various widths.
/*
* The width of the CRC calculation and result.
* Modify the typedef for a 16 or 32-bit CRC standard.
*/
typedef uint8_t crc;
#define WIDTH (8 * sizeof(crc))
#define TOPBIT (1 << (WIDTH - 1))
crc
crcSlow(uint8_t const message[], int nBytes)
{
crc remainder = 0;
/*
* Perform modulo-2 division, a byte at a time.
*/
for (int byte = 0; byte < nBytes; ++byte)
{
/*
* Bring the next byte into the remainder.
*/
remainder ^= (message[byte] << (WIDTH - 8));
/*
* Perform modulo-2 division, a bit at a time.
*/
for (uint8_t bit = 8; bit > 0; --bit)
{
/*
* Try to divide the current data bit.
*/
if (remainder & TOPBIT)
{
remainder = (remainder << 1) ^ POLYNOMIAL;
}
else
{
remainder = (remainder << 1);
}
}
}
/*
* The final remainder is the CRC result.
*/
return (remainder);
} /* crcSlow() */
Listing 2. A more portable but still naive CRC implementation
Byte by Byte
The most common way to improve the efficiency of the CRC calculation is to throw memory at the problem. For a given input remainder and generator polynomial, the output remainder will always be the same. If you don't believe me, just reread that sentence as "for a given dividend and divisor, the remainder will always be the same." It's true. So it's possible to precompute the output remainder for each of the possible byte-wide input remainders and store the results in a lookup table. That lookup table can then be used to speed up the CRC calculations for a given message. The speedup is realized because the message can now be processed byte by byte, rather than bit by bit.
The code to precompute the output remainders for each possible input byte is shown in Listing 3. The computed remainder for each possible byte-wide dividend is stored in the array crcTable[]. In practice, the crcInit() function could either be called during the target's initialization sequence (thus placing crcTable[] in RAM) or it could be run ahead of time on your development workstation with the results stored in the target device's ROM.
crc crcTable[256];
void
crcInit(void)
{
crc remainder;
/*
* Compute the remainder of each possible dividend.
*/
for (int dividend = 0; dividend < 256; ++dividend)
{
/*
* Start with the dividend followed by zeros.
*/
remainder = dividend << (WIDTH - 8);
/*
* Perform modulo-2 division, a bit at a time.
*/
for (uint8_t bit = 8; bit > 0; --bit)
{
/*
* Try to divide the current data bit.
*/
if (remainder & TOPBIT)
{
remainder = (remainder << 1) ^ POLYNOMIAL;
}
else
{
remainder = (remainder << 1);
}
}
/*
* Store the result into the table.
*/
crcTable[dividend] = remainder;
}
} /* crcInit() */
Listing 3. Computing the CRC lookup table
Of course, whether it is stored in RAM or ROM, a lookup table by itself is not that useful. You'll also need a function to compute the CRC of a given message that is somehow able to make use of the values stored in that table. Without going into all of the mathematical details of why this works, suffice it to say that the previously complicated modulo-2 division can now be implemented as a series of lookups and XORs. (In modulo-2 arithmetic, XOR is both addition and subtraction.)
Follow a Bug-Killing Embedded C Coding Standard
A function that uses the lookup table contents to compute a CRC more efficiently is shown in Listing 4. The amount of processing to be done for each byte is substantially reduced.
crc
crcFast(uint8_t const message[], int nBytes)
{
uint8_t data;
crc remainder = 0;
/*
* Divide the message by the polynomial, a byte at a time.
*/
for (int byte = 0; byte < nBytes; ++byte)
{
data = message[byte] ^ (remainder >> (WIDTH - 8));
remainder = crcTable[data] ^ (remainder << 8);
}
/*
* The final remainder is the CRC.
*/
return (remainder);
} /* crcFast() */
Listing 4. A more efficient, table-driven, CRC implementation
As you can see from the code in Listing 4, a number of fundamental operations (left and right shifts, XORs, lookups, and so on) still must be performed for each byte even with this lookup table approach. So to see exactly what has been saved (if anything) I compiled both crcSlow() and crcFast() with IAR's C compiler for the PIC family of eight-bit RISC processors. 1 I figured that compiling for such a low-end processor would give us a good worst-case comparison for the numbers of instructions to do these different types of CRC computations. The results of this experiment were as follows:
- crcSlow(): 185 instructions per byte of message data
- crcFast(): 36 instructions per byte of message data
So, at least on one processor family, switching to the lookup table approach results in a more than five-fold performance improvement. That's a pretty substantial gain considering that both implementations were written in C. A bit more could probably be done to improve the execution speed of this algorithm if an engineer with a good understanding of the target processor were assigned to hand-code or tune the assembly code. My somewhat-educated guess is that another two-fold performance improvement might be possible. Actually achieving that is, as they say in textbooks, left as an exercise for the curious reader.
CRC standards and parameters
Now that we've got our basic CRC implementation nailed down, I want to talk about the various types of CRCs that you can compute with it. As I mentioned last month, several mathematically well understood and internationally standardized CRC generator polynomials exist and you should probably choose one of those, rather than risk inventing something weaker.
In addition to the generator polynomial, each of the accepted CRC standards also includes certain other parameters that describe how it should be computed. Table 1 contains the parameters for three of the most popular CRC standards. Two of these parameters are the "initial remainder" and the "final XOR value". The purpose of these two c-bit constants is similar to the final bit inversion step added to the sum-of-bytes checksum algorithm. Each of these parameters helps eliminate one very special, though perhaps not uncommon, class of ordinarily undetectable difference. In effect, they bulletproof an already strong checksum algorithm.
|
|
CRC-CCITT
|
CRC-16
|
CRC-32
|
|
Width
|
16 bits
|
16 bits
|
32 bits
|
|
(Truncated) Polynomial
|
0x1021
|
0x8005
|
0x04C11DB7
|
|
Initial Remainder
|
0xFFFF
|
0x0000
|
0xFFFFFFFF
|
|
Final XOR Value
|
0x0000
|
0x0000
|
0xFFFFFFFF
|
|
Reflect Data?
|
No
|
Yes
|
Yes
|
|
Reflect Remainder?
|
No
|
Yes
|
Yes
|
|
Check Value
|
0x29B1
|
0xBB3D
|
0xCBF43926
|
Table 1. Computational parameters for popular CRC standards
To see what I mean, consider a message that begins with some number of zero bits. The remainder will never contain anything other than zero until the first one in the message is shifted into it. That's a dangerous situation, since packets beginning with one or more zeros may be completely legitimate and a dropped or added zero would not be noticed by the CRC. (In some applications, even a packet of all zeros may be legitimate!) The simple way to eliminate this weakness is to start with a nonzero remainder. The parameter called initial remainder tells you what value to use for a particular CRC standard. And only one small change is required to the crcSlow() and crcFast() functions:
crc remainder = INITIAL_REMAINDER;
The final XOR value exists for a similar reason. To implement this capability, simply change the value that's returned by crcSlow() and crcFast() as follows:
return (remainder ^ FINAL_XOR_VALUE);
If the final XOR value consists of all ones (as it does in the CRC-32 standard), this extra step will have the same effect as complementing the final remainder. However, implementing it this way allows any possible value to be used in your specific application.
In addition to these two simple parameters, two others exist that impact the actual computation. These are the binary values "reflect data" and "reflect remainder". The basic idea is to reverse the bit ordering of each byte within the message and/or the final remainder. The reason this is sometimes done is that a good number of the hardware CRC implementations operate on the "reflected" bit ordering of bytes that is common with some UARTs. Two slight modifications of the code are required to prepare for these capabilities.
What I've generally done is to implement one function and two macros. This code is shown in Listing 5. The function is responsible for reflecting a given bit pattern. The macros simply call that function in a certain way.
#define REFLECT_DATA(X) ((uint8_t) reflect((X), 8))
#define REFLECT_REMAINDER(X) ((crc) reflect((X), WIDTH))
uint32_t
reflect(uint32_t data, uint8_t nBits)
{
uint32_t reflection = 0;
/*
* Reflect the data about the center bit.
*/
for (uint8_t bit = 0; bit < nBits; ++bit)
{
/*
* If the LSB bit is set, set the reflection of it.
*/
if (data & 0x01)
{
reflection |= (1 << ((nBits - 1) - bit));
}
data = (data >> 1);
}
return (reflection);
} /* reflect() */
Listing 5. Reflection macros and function
By inserting the macro calls at the two points that reflection may need to be done, it is easier to turn reflection on and off. To turn either kind of reflection off, simply redefine the appropriate macro as (X). That way, the unreflected data byte or remainder will be used in the computation, with no overhead cost. Also note that for efficiency reasons, it may be desirable to compute the reflection of all of the 256 possible data bytes in advance and store them in a table, then redefine the REFLECT_DATA() macro to use that lookup table.
Tested, full-featured implementations of both crcSlow() and crcFast() are available for download. These implementations include the reflection capabilities just described and can be used to implement any parameterized CRC formula. Simply change the constants and macros as necessary.
The final parameter that I've included in Table 1 is a "check value" for each CRC standard. This is the CRC result that's expected for the simple ASCII test message "123456789". To test your implementation of a particular standard, simply invoke your CRC computation on that message and check the result:
crcInit();
checksum = crcFast("123456789", 9);
If checksum has the correct value after this call, then you know your implementation is correct. This is a handy way to ensure compatibility between two communicating devices with different CRC implementations or implementors.
Acknowledgement
Through the years, each time I've had to learn or relearn something about the various CRC standards or their implementation, I've referred to the paper "A Painless Guide to CRC Error Detection Algorithms, 3rd Edition" by Ross Williams. There are a few holes that I've hoped for many years that the author would fill with a fourth edition, but all in all it's the best coverage of a complex topic that I've seen. Many thanks to Ross for sharing his expertise with others and making several of my networking projects possible.
Additional Resources
Download Barr Group's CRC Code-C (Free)
Related Barr Group Courses:
Embedded Linux Customization and Driver Development
For a full list of Barr Group courses, go to our Course Catalog.
Footnotes
[1] I first modified both functions to use unsigned char instead of int for variables nBytes and byte. This effectively caps the message size at 256 bytes, but I thought that was probably a pretty typical compromise for use on an eight-bit processor. I also had the compiler optimize the resulting code for speed, at its highest setting. I then looked at the actual assembly code produced by the compiler and counted the instructions inside the outer for loop in both cases. In this experiment, I was specifically targeting the PIC16C67 variant of the processor, using IAR Embedded Workbench 2.30D (PICmicro engine 1.21A).
This column was published in the January 2000 issue of Embedded Systems Programming. If you wish to cite the article in your own work, you may find the following MLA-style information helpful:
Barr, Michael. "Slow and Steady Never Lost the Race," Embedded Systems Programming, January 2000, pp. 37-46.



